X/ENS Modélisation PSI 2006

MODÉLISATION EN SCIENCES PHYSIQUES
ET SCIENCES DE L'INGENIEUR

DURÉE: 5 HEURES

Aucun document n 'est autorisé.

L 'usage de calculatrices électroniques de poche à alimentation autonome, non 
imprimantes et sans
document d'accompagnement, est autorisé, une seule à la fois étant admise sur 
la table ou le poste de
travail, et aucun n 'échange n 'est autorisé entre les candidats.

Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur 
d'énoncé, il le signale sur
sa 00pie et poursuit sa composition en expliquant les raisons des initiatives 
qu'il est amené à prendre.

Le sujet comporte 16 pages

Ce sujet se propose de donner une première approche du problème du con-
trôle de vibration pour les structures élancées. Il s'agit, par exemple, 
d'éviter
les résonances destructives pour un pont en construction dont une extrémité du
tablier pend dans le vide. Pour cette première étude, on rarnënera le problème à
l'étude d'une poutre. La première partie aborde la modélisation d'un tel milieu,
la seconde l'étude vibratoire, la troisième propose une discrétisation du prob-
lème de manière à aborder dans la quatrième partie la détection et le contrôle
de l'état de la structure. Malgré la progression logique précédemment exposée,
ces parties peuvent être traitées indépendamment.

Figure 1: Géométrie d'une poutre au repos

Notations générales

0 Soit une fonction f(cc, t) de la variable d' espace a: et de la variable de
temps t, on note f la dérivée partielle par rapport au temps de f: f= --1

o Pour une matrice (ou un vecteur) M, on note M ' la transposée de cette
matrice.

1 Étude du modèle de poutre

1.1 Hypothèses, vocabulaire et notations

Géométrie
Une poutre est un milieu solide dont une dimension est très supérieure aux
deux autres (on parle de structure élancée). On se place ici dans le cadre
simple où, au repos, la poutre est un prisme droit à section rectangulaire
On munit la poutre d'un repère naturel cartésien (O, ÎÊ, Î, _') où 0 est
le centre de la face de gauche, on note (voir figure 1):

. L longueur de la poutre (a: E [O, L]) ;

0 h demi--hauteur de la poutre (y EUR [----h, h]) ;

o b demi--profondeur de la poutre (2 EUR [--b, b]) ;
0 S aire des sections ;

. Sm ensemble des points d'abscisse a: au repos ("section droite");

0 G,; centre de Sac ;
0 I' = {G...oe EUR [O,L]} "ligne moyenne".

Inertie
On suppose la poutre homogène sur chaque section et on note :

o p la masse linéique de la poutre (kg/m);

. JZ moment d'inertie linéique de la section Sm autour de (G,...7)
(kg.m).

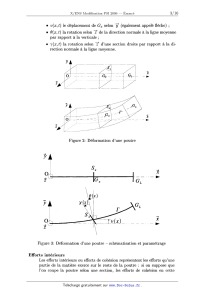
Cinématique (déformations)
On s'intéresse à un problème de flexion plane : la ligne moyenne se déforme
dans le plan (ÎÊ,Î), et on suppose que les allongements selon ?? sont
négligeables (voir figure 2). L'hypothèse fondamentale est que chaque
section Soe reste plane au cours de la transformation. On introduit

alors pour chaque instant t (voir figure 3) :

. v(a:, t) le déplacement de Goe selon îÎ (également appelé flèche) ;

. 9(sc, t) la rotation selon ? de la direction normale à la ligne moyenne
par rapport à la verticale ;

. 7(a:, t) la rotation selon ? d'une section droite par rapport à la di--
rection normale à la ligne moyenne.

Figure 2: Déformation d'une poutre

Figure 3: Déformation d'une poutre -- schématisation et paramétrage

Efforts intérieurs
Les efforts intérieurs ou efforts de cohésion représentent les efforts qu'une

partie de la matière exerce sur le reste de la poutre : si on suppose que
l'on coupe la poutre selon une section, les efforts de cohésion en cette

section sont les efforts qu'il faudrait appliquer sur la partie gauche de la
poutre pour que son état ne soit pas modifié. Etant donnée la cinématique
de sections rigides, on peut modéliser les efforts de cohésion sur chaque
section par un torseur Ç(a:, t). Ç(oe, t) représente donc les efforts appliqués
sur la partie gauche de la section SOE par la partie droite. Les éléments de
réduction de Ç(æ, t) sont une résultante T(oe, t)ÎÎ (effort tranchant) et un
moment en Gm (moment fléchissant) M (a:, t)? (voir figure 4).

Figure 4: Schématisation des efforts intérieurs sur la section Soe

Efforts extérieurs
Pour solliciter la poutre en flexion, on considère un effort linéique réparti

p(oe, t)Î, appliqué sur l'ensemble de la poutre, et un éventuel effort con--
centré F (t)--ÿ> appliqué sur l'extrémité droite de la poutre (point G L), voir
figure 5. Notamment p(oe,t) peut servir à modéliser le poids de la
poutre.

' /, p(x,t)ÿ
o®'/lk l\+\ Î 3__7__ E
E GL

Figure 5: Schématisation des efforts extérieurs répartis et concentrés

Petites perturbations
L'hypothèse des petites perturbations consiste à supposer les déplacements

et les déformations suffisamment petits pour pouvoir raisonner sur la con-
figuration au repos pour obtenir les équations d'équilibre, et pour pouvoir

assimiler la dérivation le long de la ligne moyenne à une dérivation par rap--
port àla variable a:. En conséquence, on peut systématiquement considérer
les angles 0 et 7 "petits" et linéariser les fonctions trigonométriques.

1.2 Préliminaires

Question 1.1 Donner les erpressions de S et Jz en fonction de h, b et p.

Question 1.2 Donner la relation différentielle entre 0(a:, t) et v(a:, t) (on 
rap-
pelle que 0(a:, t) << 1). 1.3 Obtention des équations d'équilibre Question 1.3 En appliquant le principe fondamental de la dynamique à un tronçon élémentaire soumis à un chargement linéique (voir figure 6), trouver deux équations aux dérivées partielles reliant u(oe, t), 9(oe, t), 7(:c, t), T(x, t), M(oe,t) et p(oe, t). Figure 6: Équilibre sous chargement réparti Question 1.4 En considérant l'équilibre d'un tronçon élémentaire & l'extrémité droite de la poutre (voir figure 7), déterminer la valeur de l 'eflort tranchant et du moment fléchissant en GL : T(L, t) et M(L,t). F(t)ÿ Ç(L--dx,t) î W\ GL--dx GL Figure 7: Equilibre sous chargement concentré à l'extrémité 1.4 Analyse locale des efforts L'objectif de ce passage est d'expliciter les champs T (ac, t) et M (a:, t) définis sur chaque section par des contributions élémentaires réparties sur chaque section. On définit ainsi en chaque point Qæ(y, z) de la section Sm (on a GOEQOE(y, z) : "") """) ° ; ; ° ' ' y y + z z ) un effort surfac1que élémentaire (on parle de vecteur contrainte, v01r figure 8): d2?æ + K(V.--.u) = 0 (12)

Question 2.6 En déduire que pouri # j, sachant que au.- ;£ wj, les modes V} et
V]- sont orthogonauæ au sens de M et K.

On introduit le quotient de Ray]eigh R :

K(u, u)

UEH, R(U)=m

(13)

Question 2.7 Que vaut le quotient de Rayleigh d'un mode propre ?
Par la suite on choisit de normer les (Vk) par la masse : M (Vk, Vic) : 1.

Question 2.8 Montrer que les modes propres rendent stationnaire le quotient
de Rayleigh ou autrement dit montrer que la différentielle de R est nulle en Vk
(on pourra s'intéresser à un champ légèrement "écarté" par rapport à un mode
propre (u : Vk + 5) et étudier les variations de R autour de Vk).

2.3 Utilisation des modes propres pour une étude transi--
toire

On admet que n'importe quel champ de H peut s'écrire comme la combinaison
linéaire de modes propres (éventuellement en nombre infini). On s'intéresse
maintenant au problème non--homogène et'on choisit de chercher une solution
v(aä,t) sous la forme suivante (le nombre de modes considérés, noté m, est un
entier fixé a priori) :

v(x. t) = 2 ...(t)...æ) (14)

Question 2.9 Par le même raisonnement qu'à la question 2.5 montrer que les
fonctions a.-- vérifient des équations difiérentielles découplées.

Question 2.10 Donner l 'expression des oz.-- pour le cas d'une poutre au repos
pourt < 0 puis soumise à un efiort concentré constant en bout de poutre. 2.4 Utilisation des modes propres pour une étude de vi- brations forcées On considère maintenant que la poutre est soumise uniquement à un effort linéique p(a:, t) et que la dépendance en temps de p est une sinusoïde de pulsation ' p(a:, t) = sin(wt)P(æ) (15) Question 2.11 Donner l'équation différentielle vérifiée par chaque coefi'icient aj. Donner l'eæpression de la solution (sans chercher à déterminer les constantes d 'intégration}. Question 2.12 Que se passe t--il quand w tend vers une pulsation propre (w --> 
un,)?
Quel est le nom de ce phénomène, quelles peuvent en être les conséquences?

3 Discrétisation duproblème

Dans le cas général d'une structure complexe, il est rare d'obtenir un modèle 
con--
tinu exploitable, on applique alors une démarche de discrétisation. De manière à
contourner le problème de la discrétisation des équations aux dérivées 
partielles,
on choisit ici de proposer deux modèles discrets distincts pour représenter, de
manière approchée, la poutre. On étudie donc une poutre décomposée de deux
manières :

o par une succession de ressorts de traction verticaux de raideur Ak reliant
des segments rigides (appelés "éléments") horizontaux de longueur AL
(voir figure 12) ; le dernier élément est chargé par un effort concentré F,

o par une succession de ressorts de torsion de raideur Ar reliant des segments
rigides (appelés "éléments") de longueur AL (voir figure 13) ; le dernier
élément est chargé par un moment de flexion M L : FL.

Figure 13: Deuxième discrétisation : ressorts de torsion

On note pour i E HO,N]] ac,- = iAL (avec a:N : L). Le segment ]oe,_1,oe,--] 
forme
le ieme élément. On appelle v,-- (t) l'ordonnée du point d'abscisse a:,- et 
9,-- l'angle
formé par le ieme élément de poutre par rapport à l'horizontale. On néglige
les actions de la pesanteur.

3.1 Formalisme séquentiel

Question 3.1 Pour la première discrétisation, écrire l'équilibre d'un élément
de poutre, en déduire une récurrence entre les v,. Ecrire l'équilibre du dernier

élément.

Question 3.2 Dans le cadre statique (accélération négligeable}, déterminer les

'U,' (2 EUR HO,NH).

Question 3.3 Pour la seconde discrétisation, calculer l'équilibre d'un élément
de poutre, en déduire une récurrence entre les (9,). Ecrire l'équilibre du 
dernier

élément.

Question 3.4 Dans le cadre statique, déterminer les (O,--), i E [[1, N ]] On 
sup-
pose Vi EUR [[1,N]] 9,-- << 1, relier les (B,) aus: (v,-) et trouver l'empression-des (U,), 'lEUR HO,N]]. Les modèles discrets sont fondamentaux pour l'étude de modèles donnés par des équations aux dérivées partielles. Un critère essentiel pour les évaluer est leur limite quand on raffine la discrétisation. Question 3.5 On s'intéresse au passage à la limite des deus discrétisations pour des problèmes statiques : 0 Vers quelle fonction de a: converge (v,) quand N ------> 00 pour la première
discrétisation (pour des raisons d'homogénéité, on posera Ak : â--Ë) ?

0 Vers quelle fonction de a: converge (v,--) quand N ----> 00 pour la deuxième
discrétisation (pour des raisons d'homogénéité, on posera Ar : %) ?

Question 3.6 Pour chaque discrétisation représenter graphiquement l'allure de
la solution pour N = 2 éléments et la limite obtenue à la question précédente.
Commenter (comparer éventuellement à la solution eæacte obtenue à la question

1.10).

Question 3.7 Pour un problème statique, on s'intéresse succinctement à un
chargement réparti constant par élément (qui se traduit dans l'équilibre d'un
élément par un second membre p,- pour les ressorts de traction ou m,-- pour les
ressort de torsion}. Pour les deux discrétisations, quelle est la régularité de
la solution si (p,--) (respectivement (m,) } tend vers une fonction continue ? 
si
(p,--) (respectivement (m,) ) tend vers une fonction continue par morceauæ ? 
Plus
que des démonstrations mathématiques, donner des interprétations physiques du
problème, éventuellement illustrées.

3.2 Formalisme matriciel

L'équilibre dynamique d'une poutre discrétisée peut se mettre sous la forme :
MV+KV=P (m)

où M et K sont des matrices carrées N >< N, Vt = (ul, . . . ,uN) et P est un vecteur représentant les efforts extérieurs (puisque u0 : 0, il peut être éliminé). Question 3.8 Donner l'expression de M, K et P pour la poutre discrétisée à l'aide de ressorts de traction, soumise à un chargement F à son extrémité droite. On admet que la matrice M est symétrique définie positive et la matrice K est symétrique. Si on reprend la définition des modes propres ( "solution har- moniques en temps du problème homogène") on trouve que la recherche de modes propres discrets se traduit par un problème aux valeurs propres général-- isé : fl£MW+K%=O (N) Question 3.9 Montrer que les hypothèses formulées précédemment sur M et K suffisent à l'existence de N valeurs et modes propres. Question 3.10 Prouuer que si ca,-- 7é wj alors Vj et V,- sont orthogonaux au sens des matrices M et K. On choisit alors systématiquement de normer les vecteurs propres par la masse (ie V,'MV,-- : 1). Pour la suite on prend des matrices de la forme : 1 2 --1 0 M=m " ,K=k"1 " " ,P=F ;(18) m -_ . _1 0 1 --1 2 1 où m et k sont des réels positifs homogènes respectivement à une masse et à une raideur (ces matrices ne correspondent pas aux discrétisations précédentes, mais conduisent à des calculs plus "légers"). On pourra noter Q : \/;'Â-. Question 3.11 Pour une discrétisation à deux éléments, calculer les valeurs et vecteurs propres du système. 4 Notions d'observabilité et de contrôlabilité On considère le système décrit par l'équation matricielle : MÜ+KV=P (w) où M est une matrice symétrique définie positive de dimension N, K est une matrice symétrique de dimension N, M et K ne dépendent pas du temps, V et P sont des vecteurs de dimension N dépendant du temps. On admet l'existence de N valeurs et vecteurs propres (w,,V,--) vérifiant -uflfia+Kw=o oeoe On admet que ces vecteurs propres sont orthogonaux au sens de M et K. Pour les applications on utilisera les matrices de l'équation (18) de dimension N = 2 (discrétisation en deux éléments). Cette partie cherche des réponses à deux questions : 0 Est--ce qu'un protocole permet de connaître l'état du système ? 0 Est-ce qu'un protocole permet de modifier l'état du système ? 4.1 Notion d'état Par état on entend non seulement la valeur des déplacements mais aussi la vitesse a un instant donné. On introduit donc la variable d'état  : (V) , qui

est donc un vecteur de dimension 2N fonction du temps.

Question 4.1 Montrer que l'évolution de (I) est gouvernée par une équation
différentielle du premier ordre que l 'on écrira sous la forme

®=AOE+Ë oen
Donner les expression de A et 15.

Question 4.2 Que devient cette équation quand on l'étudie dans la base des
modes propres V(t) : Z,Ï=1 Vkak(t) ? Quelle est l'eæpression des matrices

associées ?

4.2 Systèmes linéaires commandés / observés

On considère ici que le chargement I3 est une commande imposée par l'utilisateur
de la forme Î'(t) : Bu(t) où u(t) est une fonction scalaire et B un vecteur
indépendant du temps. On considère également qu'un appareil de mesure sché--
matisé par un vecteur ligne D permet de capter une information scalaire w(t)
sur l'état du système. Autrement dit :

A<Ï> + Bu (22)


w D

Question 4.3 Donner l 'eæpression de (t) pour t > 0 avec (O) : OEd donné.

4.2.1 Stabilité

Un système est dit stable, si et seulement si pour toute condition initiale 
d et
pour toute commande u(t) bornée, l'état (t) reste borné.

Question 4.4 Montrer que le système est stable si et seulement si toutes les
valeurs propres de A sont à partie réelle négative. On pourra utiliser la dé-
composition de l'espace en sous--espaces propres de A et étudier l'évolution du

système sur chacun de ces sous-espaces.

Question 4.5 Le système de la poutre discrétisée en deua: éléments est-il 
stable?
Interpréter le résultat.

On note pour la suite le polynôme caractéristique de la matrice A sous la

forme
FA(A) = det(A -- AI) = A" + a1/\2N"1 + - . . + a... (23)

4.2.2 Commandabilité

Le système (22) est dit commandable si, pour tout couple d'états (d,a), il
existe un temps T fini, ainsi qu'une commande u(t), t E [O, T], qui appliquée au
système est telle que ((O) : d) implique ((T) : (Da).

L'objectif ici est de démontrer que (22) est commandable si et seulement si
la matrice de commandabilité

c = {BAE A2N--IB} (24)
est de rang 2N .

Question 4.6 Montrer que (22) est commandable si et seulement si la matrice

T
QC(T) : [, esABBtesA'ds (25)

est définie pour au moins une valeur de T strictement positive.

Question 4.7 Montrer que si T > O, QC(T) est définie si et seulement si G est
de rang 2N .

Question 4.8 Quelle est la matrice B associée à un efiort imposé en bout de
poutre ? Montrer qu'un tel système est commandable.

De manière à élaborer un contrôleur le plus simplement possible, on se place
dans une base adaptée (dite base canonique commandable).

Question 4.9 Montrer que, si le système (22) est commandable, il eoeiste un
changement de repère Pc tel que :

A, : PcAPc--1
{BC : PCB (26)
avec
0 0 1 0 0
BC = : , et AC : . . . . 0 (27)
0 0 . . . . . . 0 1
1 --02N . . . . . . --CL2 ----a1

Pour ce faire, on pourra considérer la dernière ligne L de l'inverse de la 
matrice
de commandabilité C et étudier des matrices du type :

L
LA (28)
LA'2'N...1
On appelle bouclage linéaire une commande pour (22) du type
u(t) = --R(t) + u(t) (29)

où le vecteur ligne R est appelé vecteur des gains de contre--réaction, et le 
scalaire
@ commande auxiliaire.

Question 4.10 Montrer, grâce au changement de base PC introduit dans la
section précédente, qu'il est toujours possible, par un choix judicieua: de R, 
de

stabiliser tout système du type (22).

Question 4.11 Proposer un bouclage linéaire R de sorte que le système de la
poutre discrétisée en deux éléments soit auto--amorti. Autrement dit, chercher 
un
bouclage R rendant la partie réelle de toutes les valeurs propres de A 
strictement
négative. On pourra, par eæemple, rendre les parties réelles toutes égales à un

même nombre strictement négatif.

4.3 Observabilité

L'objectif de l'étude de l'observabilité est de déterminer dans quelle mesure 
il est
possible de reconstituer l'état complet d'un système dont on n'observe qu'une

partie.
Kalman a montré que cette notion est duale de la commandabilité. Il n'y

a dès lors aucune surprise à ce que les questions suivantes (et leurs réponses)
calquent les résultats établis dans la section précédente.
(22) est dit observable si pour tout d, il existe un temps T fini tel que si
(O) : d, alors la connaissance de '(/)(t) sur [G, T] permet de calculer 
d.
L'objectif des deux prochaines questions est de démontrer que (22) est ob--
servable si et seulement si la matrice d'observabilité suivante est de rang 2N :

D

o = DA (30)

D Àé1v--1
Question 4.12 Montrer que (22) est observable si et seulement si la matrice

T
QO(T) =/0 eSAtD'DeSAds (31)

est définie pour au moins une valeur de T strictement positive.

Question 4.13 Démontrer la condition d'observabilité (on pourra invoquer le
résultat obtenu à la question 4.7}.

Question 4.14 On choisit d'observer le déplacement en bout de poutre. Quelle
est la matrice D associée ? Montrer que le système est observable.

Question 4.15 Si la paire (A, D) est observable, montrer qu'il emiste une ma--
trice inversible Po, telle que les matrices A et D, dans la base induite par PO
s'écrivent :

AO Po AP5 1

avec
Ü . . . . . . 0 --a2N
1
AO : 0 Do : (Ü 0 1) (33)
0 ----a2

Ayant caractérisé l'observabilité d'un système linéaire, se pose la question
de parvenir à construire un système équivalent au système complet, construit
uniquement à partir d'observations partielles. Pour cela, on introduit un 
obser--
vateur (I) de (1), c'est--à--dire une quantité qui converge vers @ quand la 
variable

temps t tend vers l'infini.
On appelle observateur asymptotique linéaire un système de la forme :

 : AÔ+Bu--AW(ib--w) (34)
w : DCI)

tel que @ tend vers (1) lorsque t ----+ oo, quelles que soient les conditions 
initiales
(O) et (O).

Question 4.16 Montrer, en se plaçant dans la base induite par Po, que tout
système linéaire commandé--observé admet un observateur asymptotique W. On

introduira l'erreur de l'observateur : e :  -- (I).

Question 4.17 Proposer un observateur asymptotique W pour la poutre dont
on observe le déplacement à l'extrémité.

4.4 Bilan commandabilité / observabilité

Grâce aux résultats démontrés dans les deux sections précédentes, on sait 
déter--
miner si un système est commandable et observable. Si tel est le cas, on sait
construire un contrôleur du système, ainsi qu'un observateur. L'idée naturelle
qui vient, est d'utiliser l'observateur, qui reconstitue l'état du système à 
partir
de mesures partielles, dans le contrôleur du système complet, qui est capable de
stabiliser le système vers toute commande prédéfinie.

Cette démarche s'appelle le principe de séparation estimation--commande.
On peut montrer que le contrôleur muni de l'observateur, stabilise le système
linéaire commandé--observable, quelles que soient les conditions initiales de 
(I) et

de (I).