X/ENS Modélisation PSI 2004
| Thème de l'épreuve | Modélisation mathématique des phénomènes de combustion et d'explosion |
| Principaux outils utilisés | théorème de Cauchy-Lipschitz, équations différentielles |
| Mots clefs | combustion, explosion |
Corrigé
: 👈 gratuite pour tous les corrigés si tu crées un compte👈 l'accès aux indications de tous les corrigés ne coûte que 5 € ⬅ clique ici
👈 gratuite pour tous les corrigés si tu crées un compte
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Énoncé complet
(télécharger le PDF)












Énoncé obtenu par reconnaissance optique des caractères
MODÉLISATION EN SCIENCES PHYSIQUES
ET SCIENCES DE L'INGENIEUR
DURÉE: 5 HEURES
Aucun document n 'est autorisé.
Pour les épreuves d'admissibilité, ! 'usage de calculatrices électroniques de
poche à alimentation
autonome, non imprimantes et sans document d'accompagnement, est autorisé, une
seule à la fois
étant admise sur la table ou le poste de travail, et aucun n 'échange n 'est
autorisé entre les candidats.
INTRODUCTION
L'épreuve se décompose en deux problèmes, à traiter de préférence dans l'ordre
proposé.
Ils concernent tous deux la modélisation mathématique des phénomènes de
combustion et
d'explosion.
Le premier problème se focalise plus particulièrement sur les réactions
explosives. Leurs
principales caractéristiques ont été étudiées au milieu du XIXeme siècle par
Van't Hoff
et Bunsen. Elles présentent la particularité d'avoir un taux de réaction qui
dépend de
manière non-linéaire et forte de la température (par opposition aux réactions
lentes dont
la dépendance est faible). Cette propriété de forte dépendance est due à une
grande énergie
d'activation de la réaction de combustion; elle se couple en général à une
forte puissance
thermique de la réaction. Dans ces conditions, un phénomène d'autocatalyse
thermique peut
se produire, provoquer l'emballement de la réaction et une très forte
augmentation de la
température; ce phénomène est appelé explosion thermique. Divers travaux
expérimentaux
ont alors conduit N .N . Semenov à développer la théorie de l'explosion
thermique dans les
années 1920 pour le cas d'un réacteur homogène. Frank--Kamenetskii a ensuite
repris cette
théorie dans le cas non--homogène et pr0posé un traitement exhaustif dans un
certain nombre
de cas.
Le but du problème I est d'introduire ces théories et de saisir les mécanismes
de base
de couplage entre le terme source thermique issu de la réaction chimique, la
conduction
thermique et les pertes thermiques au bord des domaines considérés. Le but est
d'obtenir les
conditions critiques d'explosion, ie. les valeurs limites de certains
paramètres qui déterminent
si le phénomène d'explosion a lieu ou non. Finalement,]e dernier point que nous
aborderons
sera le couplage entre l'explosion thermique et la convection naturelle en
présence du champ
de gravitation. Ces études sont importantes et trouvent de nombreuses
applications dans la
détermination des conditions de sécurité pour le stockage de matières
dangereuses.
Dans le problème 1, nous nous contentons de considérer des phénomènes explosifs
localisés
mais nous ne traitons pas leur propagation car il s'agit d'un problème
essentiellement plus
difficile qui nécessite de prendre en compte les effets de densité volumique de
masse et de
pression puisque des ondes de chocs ou de détonations peuvent se former. On
s'intéresse par
contre, dans le problème II, à un modèle simple de déflagration à pression
constante qui
décrit la propagation d'une flamme à faible vitesse par rapport à la vitesse du
son. L'étude
fondatrice dans ce domaine date de 1928 avec les travaux de Zeldovich sur un
modèle que
nous allons étudier.
Notation : Dans toute l'épreuve, on utilisera les notations suivantes pour les
dérivées,
dtçb(t) désigne la dérivée temporelle à l'instant t de la fonction t r-->
çô(t), â&(t,x), ôfl>(t,æ)
et âæxd>(t,æ) désignent respectivement la dérivée partielle par rapport au
temps, la dérivée
partielle par rapport à la variable spatiale :r et la dérivée seconde par
rapport à la variable
m, au point (t,:c) du champ (t,:r) +---> (t,æ).
Note : Le premier problème requiert l'utilisation du théorème de
Cauchy--Lipschitz. Il est
rappelé dans l'énoncé.
PROBLÈME I
I PRÉSENTATION
Nous allons dans un premier temps considérer les équations qui régissent
l'écoulement
d'un mélange gazeux réactif compressible dans un domaine bi-dimensionnel 0, Q
(: R'. Le
candidat ne devra pas être impressionné par la complexité du système car les
quatre premières
parties se concentrent sur des versions très simplifiées pour lesquelles le
mouvement hydro--
dynamique du mélange est supposé inexistant (la vitesse du fluide est zéro,
uniformément en
temps et en espace).
Ce type d'écoulement est régi par un système d'équations aux dérivées
partielles pour
lequel le vecteur des variables est M : (pl, . . . ,p... u, v, T)t, où '
désigne la transposition et où pk
est la densité volumique de masse partielle de la kème espèce, k variant de 1 à
n, p : 22=1 p,...
la densité volumique de masse totale-, u et 11 les composantes de la vitesse du
fluide dans les
directions x (horizontale) et z (verticale) et enfin T, la température du
fluide. Ces quantités
dépendent donc du temps et des coordonnées d'espace : u : U(t,æ,z). Il n'est
pas nécessaire
de détailler ce système d'équations, mais il faut souligner qu'il doit être
accompagné par des
relations thermodynamiques et une loi d'état. Cette loi d'état relie la
pression (qui apparaît
dans les équations pour la vitesse à travers son gradient) à la densité
volumique de masse
totale, à la température et à la composition du mélange gazeux. On peut alors
écrire une
équation sur le champ de température T(t, a:, 2) qui prend la forme :
pcpô'tT+pcp(uôzT+vôzT) == V-(j...) +H+ôtp+uôæp+vôzp+l'. (1.1)
où cp est la capacité thermique massique à pression constante, Il représente la
puissance des
forces de viscosité, j..., le vecteur densité volumique de courant thermique et
V - j... désigne
sa divergence, P, la puissance thermique (terme source) due aux réactions
chimiques. '
La pression p vérifie la loi d'état des mélanges de gaz parfaits :
k
, (1.2)
"3:k_
1
m m 1 mk
où mk est la masse molaire de la keme espèce, fit la masse molaire moyenne du
mélange, R la
constante universelle des gaz, Y,c : pk / p la fraction massique de l'espèce la
et on a ZÏ=1 Y,c : 1,
II
par définition de p. Cette loi est la simple généralisation de la loi d'état
des gaz parfaits à un
mélange gazeux.
Le système de base que nous venons d'évoquer est souvent utilisé dans
l'approximation
de Oberbeck-Boussinesq qui considère que la pression et la densité volumique de
masse sont
quasiment constantes p -- po << Po et p -- po << po (le signe << signifie "très petit devant" et P0 i.e. que cette expression peut être approchée formellement par 1, ou encore que les variations indique une séparation d'échelles. Ce genre d'hypothèse implique par exemple que 1+ ° oe 1, de pression ou de densité volumique de masse par rapport à un état de référence po ou Po , sont négligeables). 1.1 On suppose que le mélange gazeux est initialement à la température T0, à la densité po et à la pression po, uniformément en espace. On néglige les différences de masse molaire, c'est--à--dire mk : m, Vk : 1, ...,n. Montrer que la loi d'état (1.2) se réduit alors à la loi d'état d'un gaz parfait simple p = p--ÆT. I.2 Montrer, en utilisant cette loi d'état, que l'approximation de Oberbeck--Boussinesq est valable pour de faibles variations de température, c'est--à--dire T -- To << To. Avant de revenir sur les équations dans la dernière partie du problème, nous allons commencer par comprendre les mécanismes de base sur des modèles simplifiés. EXPLOSION ADIABATIQUE HOMOGÈNE Le but de cette partie est de faire apparaître, dans la cadre d'une modélisation minimale, l'échelle de temps du problème. On se place dans le cadre d'une chimie simple, c'est-à--dire, d'une chimie constituée d'une unique réaction globale irréversible "Fuel ---->
Produits". Le
degré d'avancement de cette réaction est donné par la variable fraction
massique de fuel :
Y(t) ; elle vaut 1 à l'instant initial quand le fuel n'a pas encore commencé à
réagir et 0 quand
tout le fuel présent dans le réacteur a été consommé en produits et en source
thermique.
La température du réacteur à l'instant initial est notée T0 et évolue du fait
de la réaction
chimique : on note T(t) la température à l'instant t. L'évolution de la
fraction massique
Y(t) et de la température T(t) est décrite par un système de deux équations
différentielles
ordinaires. Elles font intervenir la vitesse de la réaction qui dépend de
manière non-linéaire
de la température. Ce modèle, donné pour décrire l'évolution du réacteur, est
valable pour
Y EUR [O, 1] et T EUR [TD,Tb] ; il s'écrit :
th : ---B e'ËET Y, (11.1)
dtT : (Tb -- To) Be"R--Ef Y. (11.2)
B est le facteur de fréquence (homogène à l'inverse d'un temps), E est
l'énergie d'activation
de la réaction, Tb la température du mélange lorsque tout le fuel est consommé;
cette
température est associée à une enthalpie de réaction, à la capacité thermique
du milieu
et à une quantité de fuel présente dans le réacteur. On suppose dans ce
problème que la
réaction est exothermique et donc que Tb -- To > 0. Par ailleurs B, E et R sont
des constantes
strictement positives. On ne prend en compte, dans ce modèle, que le chauffage
du milieu par
la réaction et l'on suppose que le système est isolé thermiquement de
l'extérieur; on parle
alors d'explosion thermique adiabatique.
Note : On donne ici un théorème utile pour la suite sous la forme d'une
adaptation du
théorème d'existence et unicité de solution de Cauchy-Lipschitz. On considère
un système
d'équations différentielles ordinaires autonome :
dt\IJ : F('I'), t > 0, (11.3)
avec \II(O) : % comme donnée initiale du problème de Cauchy et \Il EUR IR".
THÉORÈME : On considère un ensemble compact Q de IR" sous la forme d'un produit
d'intervalles fermés Q : [al,b1] x [a2,b2] >< [a... bn], avec a,- < b,--, i = l, . . . ,n. On suppose que F applique il dans IR", que F est C'", k 2 O, Lipschitz sur Q et que % appartient à (2. On fait par ailleurs l'hypothèse que dans le cas où la donnée initiale \Ilo appartient à (90, la frontière de 9, le vecteur F(\Ito) est soit nul (point singulier) soit non dirigé vers l'extérieur du domaine Q. Alors il existe une unique solution maximale \I! (t), t > O, du système
(11.3 ) de régularité
C'"+1 sur un intervalle de temps [O,tmaxli avec éventuellement tmax : +oo,
telle que \Il (t) EUR 9.
Dans le cas où t...... est fini, on a \Il (t) ----> n, # EUR ôfl, quand t ---->
tu,".
COROLLAIRE : Sous les hypothèses du théorème précédent, si deux solutions % et
% du système (II.3) sont égales en un instant to, \I'1(to) : %(to) : x, même si
x EUR 80 (par
exemple si to : 0 ou si to est un temps d'existence maximal fini), alors ces
deux solutions sont
égales sur l'intersection des intervalles de temps d'existence des deux
solutions maximales.
L'idée sous--jacente est que sous des hypothèses de régularité de F, deux
solutions distinctes
du système (11.3) ne peuvent pas "se croiser" dans le domaine Q.
11.1 Le but de cette question est de montrer l'existence d'une solution pour
tout temps et
d'obtenir des renseignements sur la structure qualitative de la solution du
système (II.1--II.2).
II.1.a Montrer que, du système (HJ-11.2), on peut déduire une équation sur une
quantité H, combinaison de Y et T , qui se conserve au cours du temps. Donner la
valeur de H.
II.1.b En déduire une équation autonome sur la variable Y(t)
et expliciter la fonction .
II.1.c En appliquant le théorème donné ci-dessus, montrer qu'il existe une
unique
solution maximale C°° sur l'intervalle de temps [O, t......[. Montrer que la
fonction Y(t)
est monotone strictement décroissante, puis que tmax : +oo. En déduire que Y(t)
est strictement positive (Indication : supposer que tmax est fini, montrer que
la seule
possibilité est que Y(t) --+ 0 quand t ----> t...ax, considérer la solution
constante égale à
zéro et conclure en utilisant le corollaire ci-dessus).
II.1.d Montrer que T(t) est monotone croissante bornée supérieurement par Tb.
II.1.e Déduire de II.1.c que la limite de Y(t) en +oo est 0.
II.1.f Représenter graphiquement le comportement qualitatif de la solution.
II.1.g Proposer une équation différentielle autonome décrivant l'évolution de la
température T(t), ne faisant pas intervenir Y, sous la forme dtT : A(T) et
donner
une expression explicite pour la fonction A(T).
La structure de la non--linéarité A(T) dans cette dernière équation sur la
température
ne permet pas une résolution analytique. Nous allons donc utiliser deux carac-
téristiques des réactions de combustion, introduites sous la forme de deux
hypothèses,
et expliciter le comportement qualitatif du système.
[HI] La réaction satisfait l'hypothèse des grandes énergies d'activation si
E/RT,,
est très grand devant 1, ce qui implique :
E
fl--Æ>>1.
[H2] La réaction satisfait l'hypothèse d'une grande enthalpie de réaction si
TI,--To >
T0 et donc : 2
RT
(Tb -- To) >> "'ÈÂ,
où RTO2 / E est appelée la température de Frank--Kamenetskii et est notée TpK.
II.1.g On se place dans le cas où Tb : BOOOK, To : 600K. Représenter sur deux
graphiques les fonctions T --> A(T) pour a = 50 et 5 = 100, et pour T E
[T0,Tb]. (Afin
de pouvoir comparer les deux non--linéarités, on divisera la fonction par sa
valeur
maximum A...ax sur l'intervalle [TD,Tb]). En comparant les valeurs de A(T)/Amax
pour
T : 1000K et pour T : 2400K, dans les deux situations et en observant les
graphiques,
expliquer ce que signifie "une forte non--linéarité dépendant de l'énergie
d'activation".
II.2 Nous allons maintenant étudier un modèle approché pour le système
(II.1--II.2).
II.2.a Adimensionner l'équation vérifiée par la température et écrire pour cela
une
équation sur la température réduite 9 = (T -- To)/TFK. Cela revient à utiliser
comme
température de référence la température initiale et comme échelle, la
température de
Frank--Kamenetskii.
II.2.b Montrer que, sous les hypothèses [H 1] et [H 2], et tant que 0 << 5, 0 peut être approchée par une fonction Ë(t), solution de l'équation différentielle : d : l exp(ë), (11.5) 7'1 M avec la condition initiale 9(0) : O. Le paramètre 17 est appelé temps d'induction et l'on donnera son expression explicite en fonction de B, R, E, T,, et T0. II.2.c Dans l'équation précédente, on a remplacé sous l'hypothèse [H 1], l'argument de l'exponentielle par 5. Reprendre cette approximation dans les variables dimensionnées et expliquer pourquoi on l'appelle "linéarisation de Frank--Kamenetskii". Il.2.d On pose 7 : t/r;; déduire de (11.5) l'équation différentielle sur ®(T) : Ô(t). Résoudre l'équation correspondante et donner une formule explicite pour @(7'). II.2.e Décrire le comportement "explosif" de cette solution. '1Ïacer l'évolution tem-- porelle de la solution Ü(t), pour t EUR [Û,T1[, et ceci selon deux échelles différentes pour l'axe des ordonnées : la première est telle que le maximum de l'axe des ordonnées est 5, et la seconde telle que le maximum est ,6 (on prendra fl égal à 50 pour l'exemple). Décrire le comportement aux deux échelles et commenter. II.2.f On appelle t1 le temps pour lequel EUR atteint 5/ 10 = 5. Exprimer la différence relative entre t1 et 71, ainsi que le pourcentage de 71 que représente t1. II.3 Il s'agit de montrer que l'équation simplifiée (11.5) est un "bon modèle" et d'en déduire le comportement qualitatif général de la solution de (II.1--II.2). II.3.a Montrer que la condition de validité 9 << ,8 n'est par contraignante en utilisant la fin de la question 11.2 et en déduire le comportement du système de départ sur l'intervalle [O,T[[. II.3.b Calculer la température correspondant au taux de réaction maximum, en valeur absolue, pour le système (II.1--IL2), sachant que le taux de réaction est le second membre de l'équation sur Y et vaut donc --B exp(--E / RT) Y. Comment se situe--t--elle par rapport à T,, ? II.3.c Quel scénario peut-on déduire sur l'évolution du système (Ill--11.2) dans la mesure où le taux de réaction maximum est atteint dans un proche voisinage de T] ? II.3.d Caractériser l'évolution du système dans le plan des variables dimensionnées (Y, T), Y EUR [0,1] et T EUR {TD,Tb] (appelé aussi plan de phase). Tracer par ailleurs les fonctions Y(t) et T(t). Décomposer l'évolution du système en trois étapes que l'on précisera. II.3.e Que se passe--t-il pour la consommation de fuel (caractérisée par la fraction massique de fuel Y) dans l'intervalle t EUR [O, T][ ? Interpréter l'hypothèse [H 2]. II.3.f Que devient l'évolution du système quand l'énergie d'activation devient de plus en plus grande ? II.3.g On choisit une application numérique avec To : SOUK, Tb : 3000K, fi : 50. On donnera la valeur de la température de P'rank--Kamenetskii et on refera les diagrammes de la question II.3.d en marquant les points particuliers suivants tels que -ttelque9=5, -- t tel que le taux de réaction est à son maximum. Commenter. (Remarque : les données numériques ne permettent pas de calculer T] explicitement; les temps seront donc exprimés en pourcentage de 77) IH TRAITEMENT DES PERTES THERMIQUES Dans la partie précédente, l'absence de perte thermique au bord du réacteur engendre systématiquement l'explosion thermique car la température ne peut qu'augmenter et attein- dre Tb (température de l'ordre de 3000K pour les réactions de combustion). Dans ces condi- tions, le modèle cesse d'être valide quand on arrive à de fortes températures dans des délais courts, car d'autres phénomènes rentrent alors en jeu (création d'ondes de pression, etc...). Nous levons ici l'hypothèse d'adiabaticité, mais conservons l'homogénéité spatiale. Dans un modèle plus réaliste que dans la partie précédente, les pertes thermiques à la frontière peu- vent empêcher l'explosion si elles compensent le terme source issu de la réaction chimique. Il s'agit de caractériser les conditions d'explosion, c'est-à--dire dans quels cas les pertes ther-- miques à la frontière empêchent l'explosion et dans quel cas elles ne suffisent pas à limiter la croissance de la température du système. Un modèle simple de perte, dans le cas d'un réacteur fermé, est de fixer la température à. la paroi à la température de réference T0. Le réacteur peut alors être modélisé par le nouveau système, pour t > O, T EUR [To/2,2Tb], Y EUR [0,1] :
th : --B e"ïïëï Y, (111.1)
dtT : (T,, -- To) Be-% Y -- Tl(T -- To), (111.2)
P
où T,, est un temps de transfert à la paroi et où l'on prend les mêmes données
initiales que
dans la partie II. On suppose que les deux hypothèses [H 1] et [H 2] sont
vérifiées.
III.1 Nous nous intéressons brièvement au comportement qualitatif général des
solutions du
système pour Y EUR [0,1] et T EUR [To/2,2Tb].
III.1.a Appliquer le théorème donné dans l'énoncé et montrer l'existence d'une
solution maximale C°° sur l'interval t EUR [O, t...ax[.
III.1.b Montrer que T > T0 sur l'intervalle ]O,tmax[ (indication : écrire une
équation
sur T : exp(t/Tp)(T -- To)). '
III.1.c Montrer que la quantité H introduite dans la partie Il n'est plus
conservée au
cours du temps par (III.1-III.2) en présence de pertes thermiques. Montrer
qu'elle est
majorée par la valeur obtenue pour H dans le cas adiabatique de la partie Il.
III.1.d Montrer que T < Tb. III.1.e Montrer, en utilisant le même type d'argument que dans la partie Il, que tmax : +00 et que Y(t) > O, Vt EUR [O, +oo[ (Indication : utiliser H 5 T,, et
montrer que la
seule possibilité, si t...... est fini, est que Y --> 0 et T --+ T* quand t -->
t...ax. Construire
alors une solution telle que Y : 0 et qui passe par le point (Y : O,T : T*) en
tmax).
III.1.f Déduire des questions qui précèdent que Y tend vers zéro à l'infini et
par
conséquent que T tend vers T0 à. l'infini.
III.1.g Donner le comportement qualitatif du système. Tracer la forme de Y(t)
et T(t).
III.1.h Adimensionner les équations (fill--111.2) en utilisant le même
adimension--
nement que dans la partie II, et en prenant comme temps adimensionné T : t/n
(donner d.Y, dT9 en fonction de Y et 0). '
\
111.2 Comme la quantité H n'est plus conservée, on ne peut plus se ramener a
une seule
équation et il subsiste alors le problème de la présence de la fraction
massique dans l'équation
sur 6 qui décrit l'influence de la consommation de fuel sur la vitesse de la
réaction chimique.
111.2.a Montrer que, sous les hypothèses [H 1] et [H2], l'équation sur 0 peut
être
approchée par :
N
dTë : exp(ë) -- q"(Û), (111.3)
N
où q'(û) : 75 et donner l'expression de 7.
111.2.b Sur quel intervalle de temps peut-on considérer que l'équation
précédente est
représentative de la physique du système (fill--111.2) ? Quelle hypothèse
implique son
utilisation sur la consommation de fuel dans cet intervalle ?
N
111.2.c Représenter sur un diagramme les graphes des deux fonctions exp(ë) et
q" (9) en
fonction de 5 pour diverses valeurs de 7. Etudier les points stationnaires de
l'équation
(111.3) définis par exp(ë) : q" (5), en fonction du rapport 7 = 77 /*r1D
Proposer trois
scénarios. On donnera en particulier la valeur critique 7cr de 7 ainsi que la
température
Ôcr du point stationnaire correspondant. Interpréter physiquement les trois cas.
111.2.d Relier 6... en variables dimensionnées, à la température de
Frank--Kamenetskii.
111.2.e Classifier et caractériser les diverses dynamiques possibles pour
l'équation
(111.3) en fonction de rapport 7. On étudiera en particulier les limites 7 --+
0 et 7 ----> +00.
111.2.f Que dire de la stabilité des points stationnaires quand ils existent
(un point
stationnaire est dit stable pour l'équation différentielle (111.3) si
l'évolution d'une
solution, dont la donnée initiale est prise dans un voisinage du point, est la
convergence
vers cet état stationnaire et instable dans le cas contraire) ?
111.3 Parmi les divers scénarios pr0posés, certains correspondent au
comportement du
système (III.1--III.2) et d'autres non. Nous allons étudier ce point dans cette
sous-partie.
111.3.a Montrer que cette corre3pondance est effective dans le cas 7 --> 0 et
faire le lien
avec la partie II.
111.3.b Pour 7 > 7... montrer que l'existence d'un état stationnaire vers
lequel converge
la solution de (111.3) implique une borne sur la température réduite 0 pour le
système
(1111-1112) et garantit la non-explosion.
111.3.c Dans le cas où il y a explosion pour l'équation (111.3), c'est-à--dire
pour 7 < 7... on estime F,, le temps d'induction non-adiabatique, par : +00 (15 ?] %] ------:------=--. 0 eXp(9) -- Q"(9) Justifier la borne d'intégration en utilisant les hypothèses. 111.3.c On cherche la limite de ce temps quand 7 tend vers 7cr par valeur inférieure. Pour cela on pose 0 Ô}, + x et 7 : 7cr(1 -- EUR) et l'on suppose & << 1 et donc x << 1 (cette dernière estimation, que l'on admettra, vient du fait que lorsque & << 1, la température s'établit en un temps de l'ordre de 1 autour de 0 = 1 et reste dans ce voisinage pendant une grande partie de la dynamique). Donner une estimation de ?; en fonction de EUR, pour { petit et montrer que ?; tend vers l'infini quand EUR tend vers 0 (indication : on écrira l'intégrale en fonction de x et {, puis on remplacera exp(x) par 1 + x + x2/2 puisque X supposé petit et enfin on utilisera l'égalité EUR + x6 + x2/2 oe { + ((X + £)/fi)2). En déduire la dynamique de l'explosion quand l'on s'approche des conditions critiques par valeur inférieure, et la représenter sur un diagramme (t,6(t)). III.3.d Que conclure sur le modèle (III.3) au voisinage des conditions critiques en terme de l'hypothèse [H2] : "on néglige la consommation de fuel et l'on suppose Y(t) % 1 sur t EUR [O,T;[" ? III.4 En fait, la restriction sur l'applicabilité du modèle quand on s'approche des conditions critiques n'a d'effet que dans un très petit voisinage inférieur de ';c,. III.4.a Présenter un diagramme des diverses évolutions temporelles possibles de la température dans le cas général du système (III.1--III.2). III.4.b Donner l'évolution dans le plan de phase (Y, T) et faire le lien avec la partie II, afin de synthétiser les scénarios possibles. III.4.c Conclure cette étude. IV LE CAS INHOMOGÈNE : DIFFUSION Nous allons maintenant considérer le cas inhomogène pour lequel les champs de température et fraction massique dépendent non seulement du temps, mais aussi de la va- riable d'espace. On se place dans le cadre particulier d'une bande infinie dans la direction horizontale a: et de hauteur 2L dans la direction z. On suppose le problème homogène dans la direction a: ce qui revient donc à travailler sur un problème monodimensionnel présenté sur la Figure 1. T : T0, pertes thermiques T : T0, pertes thermiques Figure 1 : Configuration On considère alors le système de deux équations aux dérivées partielles suivant : 6,Y - DôzzY : --Be--r% Y, (IV. 1) ô,T -- D a,,cr : (T,, -- To) B e-:% Y, (IV.2) où ôzz désigne la dérivée partielle seconde en la variable d'espace, 8, la dérivée partielle en temps, avec les conditions initiales Y(O,z) : 1 et T(O,z) : To, pour tout z EUR [O,2L] et les conditions aux limites T(t,0) : T(t,2L) : T0 et ôzY(t,0) : ôzY(t,2L) : 0. La condition aux limites sur Y impose la non pénétration du fuel dans la paroi du tube et le fait d'imposer la température au bord induit des pertes thermiques. On peut alors montrer qu'il existe une solution régulière C°° de ce système pour 2 EUR [0,2L], t EUR [O,+oc[, telle que Y(t,z) EUR [0,1], T(t, 2) EUR [T0,Tb[ et telle que la fonction z --+ T(t, z) est concave pour tout t EUR [O, +oo[. IV.] IV.1.a Ecrire une équation d'évolution sur la moyenne Y(t) : -21Î 02L Y(t,z)dz de Y 2 OL T(t,z)dz, celle de T. sur l'intervalle [O, 2L] et sur T(t) : 51Î IV.1.b En utilisant les conditions aux limites, le signe de T -- T0, et donc le signe du gradient de T aux limites en 2 = 0 et z : 2L, évaluer les champs de température et de fraction massique à la limite t ---> +oo.
IV.1.c Faire le lien avec le modèle homogène de la partie III.
IV.2 On introduit un temps de diffusion T,... = L2 /D, ainsi que A : re.../n,
son rapport au
temps d'induction introduit dans la partie II. En utilisant L comme échelle de
longueur, en
notant EUR = z/L, T : t/r;, et 0 défini comme précédemment, donner la forme
adimensionnée
de l'équation aux dérivées partielles sur 9 lorsque l'on néglige la
consommation de fuel et que
l'on prend Y 5 1 comme nous l'avons fait auparavant. La mettre sous la forme
a,9 - -î-a,,e : exp(0), (IV.2)
où on explicitera et justifiera le calcul de À.
\
IV.3 Donner une expression analytique implicite de l'état stationnaire 0"(5)
associé a
l'équation (IV.3) (indication : remarquer que l'équation différentielle sur 9"
en & admet
une intégrale première en multipliant par la dérivée, utiliser la symétrie et
la concavité pour
caractériser ng" en EUR = 1 au centre du réacteur. La seconde intégration se
fait par changement
de variable adéquat d>2(EUR) = exp(9""(l)) -- exp(9"(£)) que l'on justifiera)
ainsi qu'une équation
du type
'P(ÛÎÂ) = À/2,
reliant A à la température maximum 022 au centre.
IV.4 Tracer et donner la forme de cette fonction \Il ; montrer qu'elle admet un
maximum et
un paramètre critique {@ : xpmax associé. En déduire, comme dans la partie III,
trois
scénarios, sur l'existence ou non de profils de température réduite
stationnaires, suivant si
A < A... A = A.;, ou A > A.....
IV.5 Dans le cas A < A... combien existe--t--il de profils stationnaires ? En se référant à la partie 111, que peut--on prédire sur leur stabilité ? V LES PHÉNOMÈNES CONVECTIFS Nous n'envisageons pas dans cette partie une étude complète des phénomènes de couplage entre l'explosion thermique dans une bande, comme dans le cas précédent, et la convection naturelle qui va se déclencher lorsque la température au centre dépasse un seuil de stabilité. Ce genre d'étude demande un ensemble de simulations numériques sur ordinateur et une investigation paramétrique. Dans ce contexte, le modèle à utiliser est un couplage entre une équation sur la température en variables adimensionnées : 1 8,0 + 11 6,0 + i") 650 : :\- (ô,...0 + 6550) + exp(0), (V. 1) où n est la variable adimensionnée dans la direction a:, et les équations de Navier-Stokes pour un fluide incompressible sur (11,17) avec un terme source, dans l'équation de la vitesse verticale adimensionnée 17, qui inclue les variations de densité volumique de masse dues au faibles variations de température. V.1 Expliquer, à la lumière des parties précédentes, pourquoi un modèle qui néglige la consommation du fuel, suppose de faibles variations de température et considère l'équation (V.l) permet de rendre compte d'une grande partie des phénomènes d'explosion pour un modèle plus complet quand les hypothèses [H 1] et [H 2] sont vérifiées. PROBLÈME II Dans ce second problème, nous allons aborder la théorie de la propagation de flammes planes laminaires. Ces objets monodimensionnel peuvent se voir, dans certains cas simples, comme des structures auto--similaires (c'est--à-dire dont le profil spatial est invariant au cours du temps) se propageant à vitesse c. ' I PRÉSENTATION Nous allons aborder ces structures que l'on appelle "ondes progressives" pour des systèmes d'équations aux dérivées partielles, en dimension un d'espace, qui modél'isent le couplage instationnaire entre des phénomènes de conduction thermique et des phénomènes de réaction chimique. Nous allons considérer une chimie simple du type "Fuel ---->
Produits" ; l'évolution
physique peut alors être décrite par celles de la fraction massique de fuel
(qui donne le degré
d'avancement de la réaction) et de la température :
ôtY - Dô...Y : -BJ(T) Y, (I. 1)
âtT -- DôuT : (T,, - To) BzZ(T) Y, (1.2)
II
pour Y EUR (0,1] et T EUR [T0,Tb]. On rappelle que @... désigne la dérivée
partielle seconde en
la variable d'espace a:, ôt la dérivée partielle en temps; Y(t,x) désigne le
champ de fraction
massique de fuel et T(t, a:) le champ de température. Par ailleurs, B est le
facteur de fréquence
homogène à l'inverse d'un temps; & est une fonction monotone de T qui vaut 0 en
T : T0.
La température du mélange où tout est brûlé de manière adiabatique est notée
Tb, comme
dans le Problème I. On suppose dans ce problème que la réaction est
exothermique et donc
que T,, -- To > 0. Par ailleurs B est une constante strictement positive. On
remarquera que
le coefficient de diffusion de masse et conduction thermique sont pris égaux
pour simplifier
l'analyse menée dans ce problème.
ONDES PROGRESSIVES
Nous allons donc chercher des profils çb(y) et 0(y), y EUR IR et une vitesse c
(c fait partie des
inconnues du problème), tels que y = a: -- et et Y(t,æ) : qb(y) et T(t,:r) :
9(y)(Tb -- T0) + T0
soient solution de (LI-1.2). Ils nous faut aussi imposer des conditions aux
limites et c'est
sur les comportements à l'infini que nous les fixons en supposant que limy_++oe
qfi(y) : 1,
limy_+_oe d>(y) : 0 et limy_,+oe 6(y) : O, limy_,_oe 0(y) : 1. Les gaz frais
sont donc du "côté
+00" et les gaz brûlés du "côté --oo". La fraction massique Y vaut 1 quand la
réaction n'a
pas eu lieu et 0 quand tout le fuel a été brûlé. On suppose que 0(y) EUR]O, 1[
et qñ(y) EUR]0, 1[. La
flamme se déplace à la vitesse inconnue 0 strictement positive, des gaz brûlés
vers les gaz
frais (Figure 2).
Figure 2 : Onde progressive
II.] De la même manière que dans le problème 1, on peut se ramener à une seule
équation
sur la température; c'est l'objet de cette question.
II.1.a Dans un premier temps, on se donne une vitesse de flamme c positive.
Ecrire le
système de deux équations différentielles ordinaires satisfaites par les deux
fonctions
d>(y) et 9(y)-
Il.1.b On note H : @ + 6. Montrer que cette quantité est constante,
c'est-à--dire
qu'elle ne dépend ni du temps ni de l'espace. Donner sa valeur. (Indication :
résoudre
l'équation différentielle satisfaite par "H en utilisant les conditions à
l'infini pour
déterminer les constantes).
II.1.c Montrer alors que le problème se réduit à une équation sur 9(y) du type
c9' + D9" + 1b(0) : O,
et donner une expression explicite pour la non--linéarité 1,1).
II.2 On suppose que l'équation sur 9 ci--dessus admet une solution régulière
C2. Montrer que
cette solution est monotone en y (indication : supposer l'existence d'un
minimum et montrer
qu'il y a une contradiction en étudiant la convexité de la solution).
11.3 Nous allons maintenant faire quelques hypothèses sur la non--linéarité @
afin de montrer
l'existence et surtout l'unicité du profil de température 6 et de la vitesse 0.
On suppose donc
qu'il existe 17 EUR]0,1[ tel que, 1,b(0) : 0 pour 6 EUR [0,17[, zp(9) > 0 pour
9 EUR [77,1[ et w(1) : O,
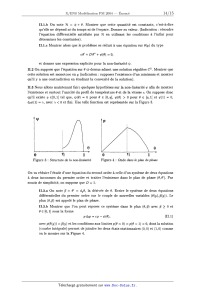
d97,[2(1) : 7, avec 7 < 0 et fini. Une telle fonction est représentée sur la Figure 3. 0 Tl 1 0 1l 1 Figure 3 : Structure de la non-linéarité Figure 4 : Onde dans le plan de phase On va réduire l'étude d'une équation du second ordre à. celle d'un système de deux équations à deux inconnues du premier ordre et traiter l'existence dans le plan de phase (9,9' ). Par soucis de simplicité, on suppose que D = 1. II.3.a On note 5 == 0' : dye, la dérivée de 0. Ecrire le système de deux équations différentielles du premier ordre sur le couple de nouvelles variables (0(y),ñ(y)). Le plan (9, p') est appelé le plan de phase. II.3.b Montrer que l'on peut reposer ce système dans le plan (0,5) avec 5 _>_ 0
et
9 E [O, 1] sous la forme
pdep = cp -- w(9), (H- 1)
avec p(9(y)) : ñ(y) et les conditions aux limites p(9 : O) : p(6 : l) = 0, dont
la solution
(courbe intégrale) permet de joindre les deux états stationnaires (0,0) et
(1,0) comme
on le montre sur la Figure 4.
II.3.c On cherche dans un premier temps a = dap(1), la pente de la solution
près du
point (1,0). On peut effectuer un développement de Taylor et supposer p : a(1
-- 9)
et v,b(9) : 7(1 --- 9), avec 7 : dæp(1). En utilisant le fait que p vérifie
l'équation (11.1),
déterminer a en fonction de c et de 7.
II.3.d On se place sur l'intervalle 9 EUR [77, 1]. On peut alors considérer
qu'à une vitesse
c donnée, on peut trouver un profil p(9) qui vérifie (11.1). Montrer que la
solution sur
cet intervalle est une fonction décroissante de c, donner l'expression de cette
solution
16 pour c = 0 ainsi que la valeur de p(n) en fonction de I : [& gb(0)d0.
II.3.e Résoudre l'équation dans l'intervalle 9 EUR [0,17[. Quel est le sens de
variation de
cette solution sur [0,17[ en fonction de c ? En déduire l'existence d'une
unique vitesse
60 telle qu'il existe une courbe intégrale continue qui joigne (0,0) et (1,0)
dans le plan
de phase (8, p). On note po(6) cette solution.
III VITESSE ET LIMITE ?) ---> 1
Nous allons maintenant donner une estimation sur la vitesse de flamme et en
déduire sa
limite dans le cas 17 ---> 1 avec I fixé.
III.] Dans cette question, on cherche à obtenir un encadrement de la vitesse de
flamme en
fonction de n.
III.1.a Montrer que co : po(n)/n.
III.1.b En utilisant les mêmes arguments que dans la partie précédente et la
fonction
?, montrer que po(n) 5 \/21.
Ill.l.c Pour obtenir une borne inférieure, utiliser la solution 2, de l'équation
différentielle :
dog = 60 -- îP(9)/ÿ(9)
sur l'intervalle 0 EUR [n, 1] avec p(1) : 0. On montrera que dans cet
intervalle p(0) 5 p0(0).
III.1.d En déduire :
Æ--col--ÛSCOSÆ,
III. 1
77 77 77 ( )
qui permet donc d'encadrer la vitesse de flamme en fonction du paramètre n.
III.2 En supposant que I reste constant en fonction de n et que l'on change
donc simplement
la forme de la non-linéarité @, que dire de la vitesse de flamme lorsque 17 -)
1 ? Que devient
alors le taux de réaction ? Donner une idée de la structure du profil de
température dans ce
cas ? Où se trouve concentrée toute la réaction ? Le profil de température
reste--t--il régulier ?
Le tracer.